handedness

26.I.1430

Drawing what they wrote on chirality and helicity.

"a standard clock, tossed with its face directed forwards, has Left-handed helicity." (wp>Chirality_(physics))

This is only a reaction note, without benefit of a fuller image yet.

The discussion of chirality and helicity ought to cover the notion of handedness and particularly parity. More importantly and as with other properties of matter (observables) it should also cover the group structure of these properties - understanding which is alas in progress.

An object has chirality if it is not identical to its mirror image. Chirality coming from the greek Chir for hand thus literally means handedness.

A chiral object will not superimpose with its mirror image. The term mirror image misleads a bit. For when I thought about this I visualized placing my left palm over a mirror which superimposed perfectly with its mirror image. Instead, what is meant is rather better described as a reflection about a basis axis.

More precisely a chiral object is not identical to itself when reflected about one axis or the other.

This reflection, an isometry transformation corresponds to a reversal of orientation.

Mathematically this is expressed by applying an orthogonal matrix to the particle's vector. The determinant of such a matrix is either 1 for a chiral object or -1 for an achiral object.

It thus that the left hand (or foot or glove or coffee mug with handle on the left) is the reflection of the right counterpart.

The electric field of a charged particle is achiral, invariant under reflection. But the magnetic field of a moving charge is revered under the reflection.

As an aside, This transformation is called an isometry because it preserves the norm (or metric) of the vector. Such reflections that either preserve or reverse orientation keep the coordinate origin fixed (it is only a reflection about a given axis). Such transformations are thus also considered Lorentz transformations, a subset of linear transformations.

The symmetry or asymmetry properties of chirality and helicity are studied through the representations of Poincare groups and their subgroup the Lorentz group, and their decomposition into further group representations. But detail on this hopefully comes later.

In the case of a Dirac-fermion that has mass such as a quark or an electron , Helicity is the projection of the spin vector S onto the momentum vector p. i.e., a dot product
h = S.p .

In the "massive" case, whereas helicity deals with whether the object transforms in an right-handed or left-handed way, chirality is the property that an object is not identical to its mirror image. Switching between an object and its mirror image is called leaves some properties unchanged such as mass. This transformation is thus a symmetry on mass (among other things) called parity.

But if there is no mass, there is also parity of spin. Ie the spin appears to be in the same direction as its axis of motion regardless of perspective (direct or mirror image). I could be wrong on this however.

When there is no mass, (and consequently no momentum) Helicity is the product of the chirality operator (which takes values -1 or 1) multiplied by

Consequently helicity has one of two values 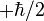and .

So if we imagine that the two clocks shown above as (massless?) fermions or particles with half-spin ,
the clock on the left is
a lefthanded clock with
chirality =-1
helicity h=
the clock on the right is
a righthanded clock with
chirality =1
helicity h=

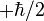
Nonetheless another page at wp (wp:Chirality_(physics)) makes an apparently contradictory statement: for a massless fermion (with spin 1/2) such as gluons, photons and gravitons, chirality is said to be the same as helicity.

Because helicity depends as it were on the state of motion of the body (massless or not), viz. the direction of its axis of motion , then it appears it is not an intrinsic property of a particle.

On the other hand, chirality which is a simple yes/no case, seems to be an intrinsic property - indpendent of the quantity or direction of motion , and likewise independent of the point of view of observer (or coordinate transformation).
- more -

acknowledgement: the image of the clock itself comes originally from a google image search thumbnail of the clock image at www-math.cudenver.edu. The thumb has been sheared vertically by 15 degrees and reflected horizontally.