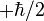04.iI.1430
cube cubus κύβος (dice) cubit كعب مكعب
and obviously الكعبة . ... Read more



* As a possible ideal: theorem graph at the deepest zoom level should include the complete set of cross references in the body of science (ie scientific literature) - though this is also a property of historical math graphs.
* thus providing on demand sequence/chain paths of book/paper citations, as well as paths of sequences of theorems
* apologetics:
* is this not already available in existing literature/existing forms, such as journal indices, encyclopedias, and books?
* yes but the graph differs in a few things
* we strip all the descriptive text and other extraneous text and information
* the whole is presented graphically (and strucurally for machines and report designs)
* the connections are made explicit and more inclusive and wide ranging than in texts enabling quick cross topic navigation by eye rather than by following links or flipping pages
* though a counteragrument is that one would still have to pan and zoom to move among paths of the graph
* we imagine a human society where each individual is a generating a field, or is the gauge particle of a field
* or that every individ is endowed with different kinds of charges.
* or rather that every individ is both a gauge particle generating a field, and endowed with different charges , "observables that interact with other particles field
* conjecture: the individuals are each unique , unlike the particles families in the physical metaphor or source of the analog we're trying to construct
* counterconjecture: not unlike physical particles, individs represent instances of different classes / families of particles (having nothing to do necessarilty with biological kinship)
* each individual generates a field of influence in its neighborhood
* others are either outside the field or inside, or the field could be infinite tapring off to infinitesimality in the case of people who do not know the individual and who might subissent a residual influence that is negligible not , felt.
* those that are closer to the indvid who generates his field, have a larger charge wrt to the charge field generated by the individ than others.
* this determines their proximity or distance to him in his field - which socially translates to the group of people interacting directly with the individ.
* what kind of topological space would correspond to the set of individuals in a society?
* how connected, compact, and separable is that topological space?
* what kind as in how is it to be classified? t0, t1, t2, t2.5, t3, t3.5 , t4, t5, t6,
* hausdorff, normal, regular, tychonoff, etc.
* we note that the intersections of neighborhoods are not empty, as one clue to the type of topology of the social spc
* we let state be the open/closed / clopen sets that constitute the (local) neighborhood of each individ in the social set or space
* there may be a prblm w/ that def
* we image that transformations are changes of state for a given subset S of the spc
* if the change of state is generated from S (self-generated) ,
* the xform is an automorphism?
* equiv to action by the subset?
* if the change is generated by another subset R , it is a xform R->S or is it?
* it is not
* we cannot change a subset R to subset S , we cannot transorm people into other people
* the changes are from state(t1) to state(t2),
* thus it seems the change is from a subset to a subset hence always an automorphism
* on the other hand individs may move from one subset to another in the course of / due to a xformat ,thus
* was the xform applied to single subset ending up affecting more than just that subst or
* was the xformat applied to all the subsets that got affected?
* thus there may be two prblms w/ xformats
* in defining what is a state
* in defining what is a transformation (of what, what changes what remains the same, from what to what,automorph or not)
* motivation for social xforms:
* ideally that would be to look at em in terms of groups, the study of which properties are useful to descriptions (and verifiable sims) of the system
* but since a) i know neither what it means to organize xforms into groups , nor what the props o groups and their representations, their lie algs and their lie algebras' reps say about the system or the xformats; and b) i am in the effort to understand and know those things
* this is what the construct of the social field analogy and identifying xformats their groups vis a vis the props / observables and the system.
* wrk symmetry into that: those xforms that leaves certain props unchanged.


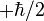 and
and  .
.